
Pythagoras
Pythagoras is a really smart guy.
People don't really know if he existed or not because there is no evidence of him ever being alive.
The artifacts were the pythagorean theorom, a square, and the R.A.T.
From last Friday, and all of this week, we have been learning about Pythagroas, and his theroey named Pytagorean Theroem. His theory is that on a R.A.T ( right angle triangle) , you can find the hypotenuse (the longest side of the triangle right on the opposite side of the right angle) by using the the measuraments of the two legs ( the two legs are what make up the right angle in the triangle). To make this easier for you to understand, we will call the two legs a and b, and the hypotenuse c. The thoroem is a squared plus b squared equals c squared. For now, I am going to say that side a is 2cm and side b is 3cm. So, since we know what sid e a and b equal already, we can put it down in our equasion. Now the equasion says, 2 squared plus 3 squared equals c squared. Since we want to get rid of the exponents, we square the numbers to get, 4 plus 9 equals c squared. Now lets add the numbers together to get an equasion of 13 equals c squared. To finish things off, lets put square roots on both sides so we can get rid of the exponent on the c. Now we come up with an answer of 3.605. Below is the same example i have just told you but in picture.
Below you is more examples of this thorey.
A checker board has 64 small squares that each have a demension of 3cm X 3cm. The 64 squares are arranged in eight rows of 8.
a. What is the length of the diagonal of a small square?
b. What is the length of the diagonal of the board?
b. What is the length of the diagonal of the board?
For this equasion, i am going to cut the small square and the big square in half. First with the little little square.



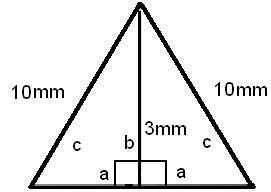
Here is another example ofthe pythagorean theorom.
This diagram shows the game plans for a game designed by Harbeck Toys INC. The board is made up of a square and four identical right triangles.
If the central square has an area of 225 square centimetres what is the perimeter of the board game? Show how you know.
For this example, I am first going to find the square root for 225 so I can get side length for a and b. I got an answer of 15. Now I am going to solve for c since I already know that they both are 15. I got an answer of 21.213. Now that I know what side c is, I can find out the perimeter of the board. All I have to do is multiply side c and side b by four, and then add the two answers that I get. I got an answer of 144.852cm. So now you know that the perimeter of the board is 144.852cm.

-Oops! Side c is suppose to be 21.213.
Now for the last example of the post.
For this example, I am going to only use one of the triangles to solve for a. The answer to a is 6.
-Oops again! The b side is suppose to be 8 cm.
These are some words that I will explain if you didn't know what they meant earlier when I said them:
Hypotenuse: The side of the triangle that is right across from the right angle. It is also the longest side. (You know that you have got the answer wrong if the hypotenuse isn't the largest side of the triangle.)
R.A.T: This stands for right angle triangle.
Legs: The sides that make up the right angle in a triangle.
Here are some things that you should know about shapes.
Rectancle: Has four right angles. All of the angles put together equal 360 degrees. It is also 2
R.A.T that has all different lengths.
Square: The same thing I said for the rectangle except it is 2 R.A.T that have the same lengths for side a and b.
R.AT (different lengths): Has one 90 degree angle, and all the angles put togther equal 180 degrees. Has two legs. (all R.A.T has to have 2 legs or else it isn't a R.A.T)
R.A.T (a and b are the same length): The same thing that I said for the other R.A.T except the
hypotenuse is always going to be 45 degrees.
Here are the videos that me and my friends made to help you understand what I was trying to teach you in this whole blog post even better.








first commenter.XD nice one jai
February 26, 2009 at 11:47 PM